COVID-19: 집단 면역은 완전한 공상인가?
현재 세계적 관심사 중 하나인 코로나19에 대한 흥미로운 관점이라 소개합니다. 일은 바쁜데 꼭 이런 전공 외적 사항만 재미있네요... 간만에 시간 쥐어짜내서 내놓은게 이런거라니... 이미 거의 안하고 있지만... 밀덕질도 접을때가 되었나 싶습니다...
본문에도 언급되어 있듯 향후 통제불능의 무제한적인 경로를 따를 때에도 작금과 같은 봉쇄조치로 감염 확산을 방어할 수 있을 지는 모르겠습니다. 여러분들은 어떻게 생각하시는지요?
─
COVID-19에 대한 집단 면역에 생각보다 일찍 도달하는 이유
서론
3월 경 임페리얼 칼리지 COVID-19 대응팀에 의해 발표된 연구 (Ferguson20[1]) 는 영국에서 막대한, 미국과 다른 나라들에 있어서는 상당한 정도로 정부 조치를 주도하는 것에 대한 원인이 되는 것으로 보인다. 해당 보고서가 등장하기 이전까지는, 영국 정부의 전략은, 최소한, 전염병의 성장을 둔화시켜 "집단 면역"을 구축하고 종국에는 그 원인을 점진적으로 제거하는 것으로 보인다.
'집단 면역 역치값' (HIT) 은 개별 감염자가 평균적으로 얼마나 많은 사람들을 감염시키는지를 측정한 전염병의 기초 재생산 속도인 R₀ 로부터 추산될 수 있다. 전염병 성장의 표준 단순 구획 모델은 HIT가 {1-(1/R₀)}와 동일함을 시사한다. HIT 지점을 지나가면, 신규 감염 속도가 감소하기 시작하여, 의료 시스템이 붕괴하지 않도록 하고 질병 제거를 위한 더 실용적인 단계를 취할 수 있도록 한다.
그러나, Ferguson20 보고서는 집단 면역에 의존할 시 유행병 확산 간 주로 2개월 기간 동안 R₀ 추정치 2.4를 기반으로 영국 및 미국 인구의 81%가 감염될 것으로 추정하였다. 본 수치는 HIT가 50~60% 사이에 있음을 의미한다[2]. 이들의 보고서는 의료 시스템이 붕괴하여 더 많은 사망자를 초래할 수 있음을 시사하였다. 이들은 가혹한 정부의 개입을 통하여 이러한 결과를 예방할 수 있음을 주장하였다. 이러한 개입은 영국 및 미국 대다수 주에서 극도로 파괴적이고 제한적인 "봉쇄"를 통하여 신속히 이행되었다.
주목할 만한 예외는 스웨덴으로, 상대적으로 약한 사회적 거리두기 정책을 기반으로 한 집단 면역 기반 전략을 계속 추구하였다. 임페리얼 칼리지 팀은 3월 중순 이러한 정책이 도입된 이후 스웨덴의 R₀는 2.5였으며, 1.5보다 낮을 확률은 2.5%에 불과하다고 추산하였다.[3] 3월 하반기 스웨덴에서의 급속한 COVID-19 확산은 R₀가 2.0보다 상당히 낮을 것 같지는 않음을 암시하였다.[4]
매우 현명하게, 스웨덴 공중보건 당국은, COVID-19가 가장 먼저 강타한 스톡홀름 주에서 PCR 검사를 통하여 SARS-CoV-2 바이러스로 인해 감염된 개개인의 유병률을 조사하였다. 그 결과 인구 17%가 4월 11일까지 감염되었고, 5월 1일까지 이는 25%로 증가하였을 것으로 추정된다.[5] 그러나 신규 환자 수는 총 입원 환자 숫자와 같이 4월 11일까지 증가세를 멈추었고,[6] 이후 양 수치 모두 상당히 감소하였다. 이 패턴은 인구의 17%만이 감염된 것으로 보이는 시점인 4월 11일에 HIT에 도달하였음을 나타낸다.
스톡홀름 주에서 단지 인구 17%만이 감염된 상태에서 HIT에 도달한 반면, R₀는 일반적으로 HIT 50%임을 시사한다.
인구 불균일의 중요성
최근 논문 (고메즈 등[7])이 그 답을 제시한다. 이들은 개개인의 감염에 대한 민감도와 타인 감염 경향의 편차가 균질한 인구에서보다 훨씬 낮을 수 있음을 보여주었다. 표준 단순 구획 전염병 모델은 이러한 변동성을 고려하지 않는다. 그리고 Ferguson20 연구에서 사용된 모델은 이보다 훨씬 더 복잡하긴 하나, 타인과의 현저한 지리적 분리 및 가구 규모와 같은, 전염병 성장에 대한 미약한 영향만을 동반하는 매우 제한된 인자들로 인하여 발생하는 불균일성을 고려하는 것으로 나타난다.[8] 고메즈 등에 의해 이러한 변동성을 고려하기 위한 수정된 구획 모델을 사용하여 민감성 및 전염성 간의 공변성을 더 현실적인 방법으로 다룰 수 있으며, HIT가 정말로 인구가 균일할 때 부다 훨씬 더 낮은 수준에 도달한 것을 확인하였다. 이는 왜 4월 중순 이후 스톡홀름에서 HIT 지점을 통과한 것으로 보이는지 설명할 것이다. COVID-19에 크게 영향을 받은 다른 주요 도시 및 지역에서도 마찬가지이다.
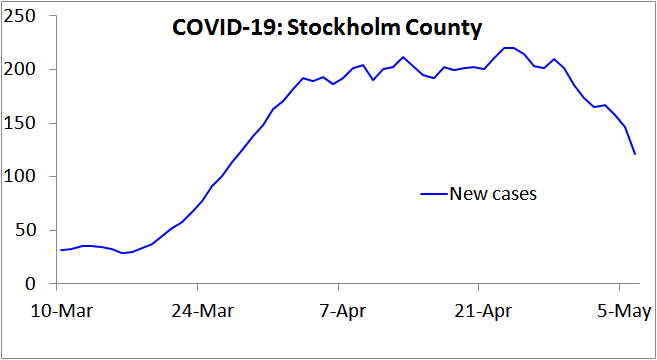
Figure 1. 표시된 날짜까지 7일 동안 스웨덴 스톡홀름 주에서 보고된 신규 COVID-19 사례. 스웨덴에서 COVID-19 감염에 대한 검사는 3월 12일에 협소화되어 병원 진료가 필요한 사람들을 대상으로 실시되었고, 그 이후 적은 비율의 감염만이 사례로 기록됨. 이는 도식된 첫 주 동안 증가세의 부재를 설명. 증상 발현에서 입원까지는 보통 수 일이 걸리며, 이러한 변화는 또한 감염과 사례 기록 간의 지연을 증가시킴. 따라서 3월 중순부터 7일간의 평균 신규 확진 수치는 약 2주일 전에 발생한 신규 감염을 반영함.
이용된 역학 모델
고메즈 등과 같이, 본인은 인구를 4개 분류로 분할하는 단순한 'SEIR' 역학 모델 [9] 을 이용하였다: Susceptible (감염되지 않음), Exposed (잠복기: 감염되었으나 전염성은 아님), Infectious (일반적으로 병에 걸림), Recovered (따라서 면역이고 무해함). 이는 그림 2에 도시하였다. 실제로, Recovered 분류에는 모델 역학에 동일한 영향을 미치는, 사망자들이 포함되어 있다. 전체 인구는 Susceptible 분류에서 시작하며, 작은 비율이 전염병 종자가 되는 Infectious 분류로 남는다. 전염성의 개인은 Susceptible 분류의 개인을 감염시켜 Exposed 분류로 이동하게 한다. Exposed 분류의 개인은 점진적으로 Infectious 분류로 전환되며 평균적으로 선택된 잠복기 동안 Exposed 분류로 남는다. Infectious 분류의 개인은 점진적으로 Recovered 분류로 전환되고, 평균적으로 선택된 감염기 동안 Infectious 분류로 남는다.
![]()
Figure 2. SEIR 역학 모델 분류 다이아그램
COVID-19의 경우, 질병(증상) 단계는 일반적으로 감염 5일 후에 도달하지만, 감염된 개인은 이틀 일찍 전염성을 띄기 시작한다. 그리하여 나는 평균 잠복기를 3일로 설정하였다.[10]
전염 기간은 주로 전염성 및 증상 발현 간의 지연과 증상 발현 시 감염자가 얼마나 신속하게 타인과의 접촉을 줄이는지, 또한 얼마나 많은 무증상 전염 사례가 존재하는지에 달려있다. SEIR 모델에서, 감염 기간은 세대 시간으로부터 잠복기를 감하여 - 원 감염자와 이들이 유발한 감염 사이의 평균 간격 - 도출할 수 있다.
Ferguson20 모델은 세대 시간을 6.5일로 가정했으며, 이후 추정치인 7.5일보다 약간 낮다.[11] 나는 COVID-19 발생 시작 시점에서의 성장률과 일치하는 7일을 사용하였다.[12] 따라서 전염 기간은 4(=7-3)일이다.
나는 Ferguson20 에서 사용된 R₀=2.4를 그대로 사용하였다. 평균적으로, 개인이 Infectious 분류에 잔류하는 동안, 이들이 감염시킨 Susceptible 분류 개개인의 수는 R₀ * {Susceptible 분류에 잔류하는 인구의 비율} 이다.
이러한 설정으로, 모든 개인이 동일 특성을 지니는, 표준 SEIR 모델을 통해 투영되는 COVID-19 전염병의 진행은 Figure 3 에 도시하였다.
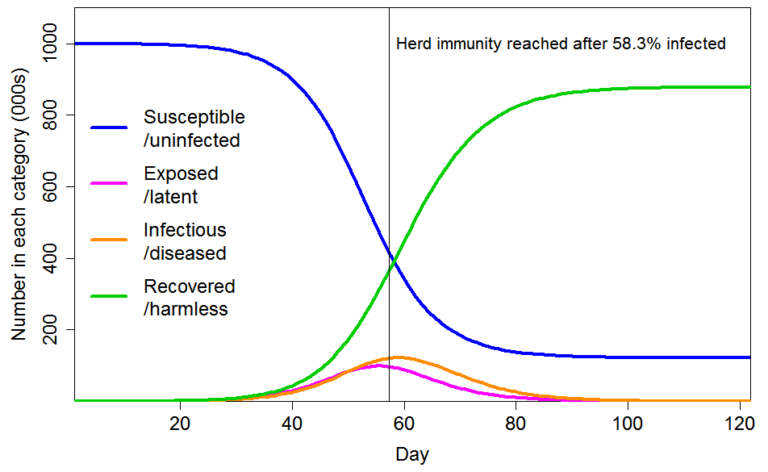
Figure 3. R₀=2.4 및 균일 인구의 SEIR 모델에서 전염병 진행. 제로 시간에서 시딩 강도에 의존하는 집단 면역 역치 도달 시간은 임의적임.
개인의 민감성 및 전염성의 변동성 반영을 위한 기본 SEIR 모델의 수정
대부분의 COVID-19 전파는 유증상 및 잠복상태의 감염자로부터 직접 발생하며, 무증상의 경우나 환경으로부터는 거의 전염되지 않는 것으로 여겨진다. [13] 소수 개인이 대다수의 감염을 차지 - '슈퍼스프레더' - 한다는 강력한 증거가 존재한다.
전파 분산에 대한 좋은 척도 - 많은 확산자를 통하여 혹은 소수만을 통하여 감염이 발생하는 정도 - 는 변동 계수 (CV) 이다.[14] COVID-19에 이 수치에 대한 두 가지 다른 추정치가 발표되었다. 심천에 기반한 연구[15]는 8.9%의 사례가 전체 감염의 80%를 차지하고, 다국적 연구[16]는 10% 사례가 차지함을 추산하였다. 양 경우 모두 이 목적을 위한 표준인 감마 확률 분포가 가정되었다. 해당 CV의 최적 추산치 및 95% 불확실성 범위는 3.3 (3.0-5.6) 및 3.1 (2.2-5.0) 이다. 이 수치는 2003년 유행병인 SARS의 추산치인 2.5보다 약간 더 높다.[17]
CV 추산치는 감염 전파 확률을 나타낸다. 이들은 타인을 감염시키는 개개인의 각기 다른 경향에 대한 인구 불균일성을 반영하나, 개인간의 민감성 차이를 얼마나 반영하는지는 불분명하다. 그러나 COVID-19 전파는 거의 대부분 개인 대 개인 전파이므로, 전파율의 불균일성 대부분은 사회적으로 개인이 얼마나 연결되어 있는지, 그리고 다른 개인들과의 상호작용이 얼마나 밀접하고 장기적이었는지를 반영한다. 이러한 인자들은 개인으로부터 및 개인에게로 전파될 확률에 영향을 미치므로, 개인 전파 가능성의 변동을 야기할 뿐만 아니라 감염에 대한 민감성에도 동일한 변동을 유발하여야 한다.
일반적으로 사회적 연결성 관련 인자는 개인의 민감성과 전염성이 양의 상관관계에 있음을 의미하며, 강한 상관이 있음을 가정하는 것이 비합리적이지 않다. 그러나 고메즈 등의 경우처럼, 개인의 전염성이 개인의 민감성과 직접적으로 비례함을 가정하는 것은 비현실적으로 보인다. (이들 모델의 다른 경우, 이들은 개인의 전염성이 이들의 민감성과 관계없음을 가정한다.)
상호작용 중 민감한 개인을 감염시킬 누군가의 가능성에 대한 일부 변동성은 바이러스 부하 크기와 같은 사회적 연결성과 무관함이 명백하다. 마찬가지로, 민감성은 개인의 면역 체계 강도와 이들의 사회적 연결성에 따라 달라질 수 있을 것이다. 나는 단위-중위수 로그정규분포를 사용하여 이러한 사회적 연결성에 관계없는 전염성과 민감성의 변동을 반영한다. 이들의 표준편차는 이들이 나타내는 인자의 강도를 결정한다. 나는 개인의 전체적 전염성을 그들의 공통적인 사회적 연결성 관계 인자와 이들(공통 사회적 연결성 관계 인자)과 관계없는 전염성-특정 인자의 산물로 모델링하고, 이에 상응하게 이들의 전반적 민감성을 계산하였다.[18]
나는 민감성 및 전염성 양측에서 불균일성을 유발하는 공통적인 사회적 연결성 인자 CV=1 및 CV=2의 경우를 고려한다. 민감성의 (사회적 연결성에) 관계없는 로그정규분포 불균일성에 대하여 나는 CV 0.417 또는 0.947에 해당하는 표준 편차 0.4 또는 0.8을 취한다. 이들의 감마-분포 불균일성 공통인자가 1로 설정된 경우, 민감성의 총 불균일성은 각각 낮거나 높은 (사회적 연결성에) 관계없는 불균일성 표준편차를 사용할 때 각각 1.17 혹은 1.65이다; 여기서 2로 설정되면, 민감성의 총 불균일성은 각각 2.17 혹은 2.98이다. 개인의 사회적 연결성에 관계없는 전염성-특이 불균일성 인자의 변동성 규모는 전염병의 진행이나 HIT에 영향을 미치지 않기 때문에, 단순화를 위하여 여기에서는 이를 생략한다.[19]
결과
Figure 4는 공통 사회적 연결성 인자의 불균일성 CV=1에 대한 COVID-19 전염병의 진행을 보여주며, 민감성의 (사회적 연결성에) 관계없는 불균일성 표준편차는 0.4이다. HIT는 23.6%로써 균질 모집단의 58.3%에 비해 60% 더 낮다. 궁극적으로는 인구의 88%가 아닌 43%가 감염된다. 민감성의 (사회적 연결성에) 관계없는 불균일성의 표준 편차가 0.8로 증가하면 HIT는 18.9%가 되고 인구의 35%가 최종적으로 감염된다.
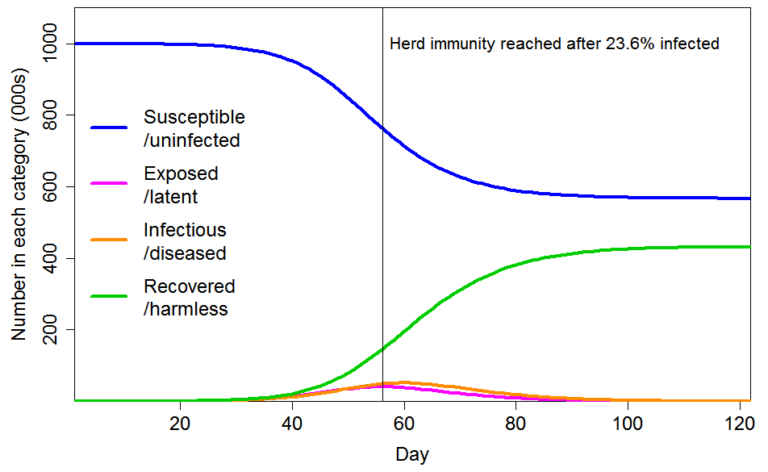
Figure 4. R₀=2.4, 민감성 및 전염성에 대한 불균일성 공통 인자인 CV=1, 민감성의 (사회적 연결성에) 관계없는 배수적 불균일성인 표준편차=0.4를 갖는 인구를 대상으로 한 SEIR 모델에서의 전염병 진행 양상
Figure 5는 공통 사회적 연결성 인자의 불균일성인 CV가 2, 민감성의 (사회적 연결성에) 관계없는 불균일성인 표준편차가 0.8인 경우의 COVID-19 전염병의 진행 양상을 도시한다. HIT는 단지 인구의 6.9%에 불과하고 궁극적으로 인구의 14%만이 감염된다. 민감성의 (사회적 연결성에) 관계없는 불균일성인 표준편차가 0.4라면 이 수치는 각각 8.6%, 17%가 된다.
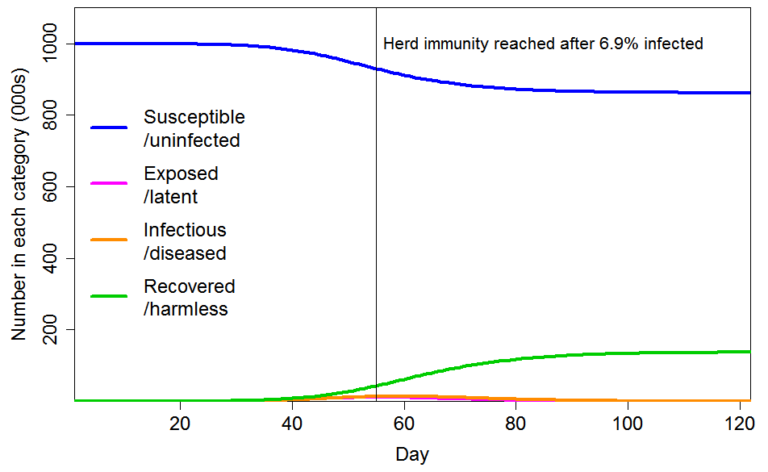
Figure 5. R₀=2.4, 민감성 및 전염성에 대한 불균일성 공통 인자 CV=2 및 민감성의 (사회적 연결성에) 관계없는 배수적 불균일성인 표준편차=0.8를 갖는 인구를 대상으로 한 SEIR 모델에서의 전염병 진행 양상
균일한 인구를 가정하지 않고 표준 SEIR 역학 모델에서 민감성 및 전염성의 불균일성을 합리적으로 통합하면, 집단 면역 역치가 크게 감소하고, 또한 만일 유행이 제한되지 않는 경로를 따를지라도 최종적인 감염 수준 또한 크게 감소한다. 따라서 집단 면역을 달성하는 데에 포함되는 사망자의 수는 그렇지 아니한 경우보다 훨씬 적다.
필자의 견해로는, 실제 집단 면역 역치는 아마 상기 Figure 4 및 5에 도시된 사례인 7%에서 24%의 사이일 것이다. 스톡홀름 주의 증거에 따라, 약 17%인 경우, HIT 도달 전의 감염으로 인한 사망자는 인구에서 매우 낮은 비율이어야 한다. 스톡홀름의 감염 치명율은 Ferguson20에 사용된 Verity 등[21]의 추정치보다 상당히 낮은 0.4% [20]이며, HIT에 도달할 때 까지 감염으로 인한 치명율은 0.1% 이하이다. R₀는 인구밀도와 양의 상관관계를 갖기 때문에, 인구밀도가 낮은 지역에서 HIT에 도달하기 위한 치명율은 더 낮아야 한다.[22] 따라서, 총 사망자는 집단 면역이 될 때까지 인구의 0.1%를 훨씬 하회하여야 한다. 비록 후속 추가 사망자가 발생할 수 있으나, 유행이 감소하면 감염 확산 예방을 위하여 검사 및 접촉 추적을 통하여 종결을 앞당기는 것이 점점 더 실현가능해져야 한다. 따라서 완전이 완화되지 않은 시나리오에서 SEIR 모델에 의해 예측되는 것보다 더 많은 사망자 수를 감소시킬 수 있어야 한다.
니콜라스 루이스 2020년 5월 10일
──────────
[1] Neil M Ferguson et al., Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team Report 9, 16 March 2020, https://spiral.imperial.ac.uk:8443/handle/10044/1/77482
[2] A final infection rate of 81% implies, in the context of a simple compartmental model with a fixed, homogeneous population, that the ‘effective R₀‘ is between 2.0 and 2.1, and that the HIT is slightly over 50%. Ferguson20 use a more complex model, so it is not surprising that the implied effective R₀ differs slightly from the basic 2.4 value that Ferguson20 state they assume.
[3] Flaxman, S. et al., Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries. Imperial College COVID-19 Response Team Report 13, 30 March 2020, https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-13-europe-npi-impact/
[4] Based on the Ferguson20 estimate of a mean generation time of 6.5 days, which appears to be in line with existing evidence, an R₀ of 2.0 would result in a daily growth rate of 2.0^(1/6.5)= 11%. That is slightly lower than the peak growth rate in cases in late March in Stockholm County, and in early April in the two regions with the next highest number of cases, in both of which the epidemic took off slightly later than in Stockholm, and in line with the growth rate in Swedish COVID-19 deaths in early April
[5] https://www.folkhalsomyndigheten.se/contentassets/2da059f90b90458d8454a04955d1697f/skattning-peakdag-antal-infekterade-covid-19-utbrottet-stockholms-lan-februari-april-2020.pdf
[6] John Burn-Murdoch, Financial Times Research, 2 May 2020. http://web.archive.org/web/20200507075628/https:/twitter.com/jburnmurdoch/status/1256712090028576768
[7] Gomes, M. G. M., et al. Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold. medRxiv 2 May 2020. https://www.medrxiv.org/content/10.1101/2020.04.27.20081893v1
[8] The 81% proportion of the population that Ferguson20 estimated would eventually become infected is only slightly lower than the 88% level implied by their R₀ estimate of 2.4 in the case of a homogeneous population.
[9] https://en.wikipedia.org/wiki/Compartmental_models_in_epidemiology#The_SEIR_model
[10] Gomes et al. instead set the latent period slightly longer, to 4 days and treated it as a partly infectious period, unlike in the standard SEIR model.
[11] Li Q, Guan X, Wu P, et al.: Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020; 382(13):1199–1207.https://www.nejm.org/doi/10.1056/NEJMoa2001316
[12] Once a SEIR model has passed its start up phase, and while a negligible proportion susceptible individuals have been infected, the epidemic daily growth factor is R₀^(1/generation time), or 1.10–1.13 for R₀=2.0–2.4 if the generation time is 7 days.
[13] L. Ferretti et al., Science 10.1126/science.abb6936 (2020).
[14] The coefficient of variation is the ratio of the standard deviation to the mean of its probability distribution. It is usual to assume a gamma distribution for infectivity, the shape parameter of which equals 1/CV2.
[15] Bi, Qifang, et al. “Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study.” The Lancet Infectious Diseases 27 April 2020. https://doi.org/10.1016/S1473-3099(20)30287-5
[16] Endo, Akira, et al. “Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China.” Wellcome Open Research 5.67 (2020): 67. https://wellcomeopenresearch.org/articles/5-67
[17] Lloyd-Smith, J O et al. “Superspreading and the effect of individual variation on disease emergence.” Nature 438.7066 (2005): 355-359. https://www.nature.com/articles/nature04153
[18] For computational efficiency, I divide the population into 10,000 equal sized segments with their common social connectivity factor increasing according to its assumed probability distribution, and allocate each population segment values for unrelated variability in susceptibility and infectivity randomly, according to their respective probability distributions.
[19] A highly susceptible but averagely infectious person is more likely to be removed from the susceptible pool early in an epidemic, reducing the average susceptibility of the pool. However, no such selective removal occurs for a highly infectious person of averagely susceptibility. Therefore, as Gomes et al. point out, variability in susceptibility lowers the HIT, but variability in infectivity does not do so except to the extent that it is correlated with variability in susceptibility.
[20] On 8 May 2020 reported total COVID-19 deaths in Stockholm County were 1,660, which is 0.40% of the estimated 413,000 of its population who had been infected by 11 April 2020. COVID-19 deaths reported for Stockholm County after 8 May that relate to infections by 11 April 2020 are likely to be approximately balanced by deaths reported by 8 May 2020 that related to post 11 April 2020 infections.
[21] Verity R, Okell LC, Dorigatti I, et al. Estimates of the severity of COVID-19 disease. medRxiv 13 March 2020; https://www.medrxiv.org/content/10.1101/2020.03.09.20033357v1.
[22] Similarly, the HIT may be significantly higher in areas that are very densely populated, have much less inhomogenous populations and/or are repeatedly reseeded from other areas. That would account for the high prevalence of COVID-19 infection that has been found in, for instance, some prisons and residential institutions or in city districts.




